Inserting Atoms Between Octahedra
 |
Recall how the regular corner shared octahedral network of the crystal structure of rhenium trioxide contained large voids or interstices. These provide obvious sites for accommodating atoms. And compounds such as tungsten trioxide (WO3) which also crystallizes in this structure can soak up metal atoms such as sodium and potassium into these large sites (in the same way as we just saw that close packed metal structure took much smaller atoms into their smaller interstitial sites). However, unlike the case of the interstitial metal compounds, the physical properties of the metal loaded tungsten trioxides are radically changed; in particular, the outermost electrons of the metal atom become delocalised imparting metallic like properties on the solid. Indeed, these compounds are often referred to as 'tungsten bronzes' because of their metallic like lustres. These bronzes contain varying amounts of inserted metal (ranging from zero to full occupancy of the void sites). They are, nevertheless, a restricted class of compounds forming with only WO3 and few other metals as the host oxide.
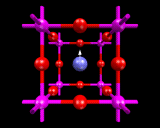
There is, however, a substantial class of compounds based on exactly the same structural principles. The archetype is the compound calcium titanate (CaTiO3) - the mineral perovskite - whose structure can be described in terms of a TiO3 corner shared network as in the ReO3 structure, with all the void sites fully occupied by Ca atoms; TiO3 is of course a hypothetical compound as Ti has a maximum valence of 4. (Titanium dioxide, TiO2, has the highest oxygen content consistent with this composition for a purely titanium and oxygen containing compound.) For this reason the chemical and physical properties of these materials are very different from the bronzes described earlier. But the structural principles are exactly the same.
Solids (and solid state chemists) have made the most of this simple idea. As we learnt earlier, a large number of metal atoms form stable MO6 octahedra which can be assembled to give the corner sharing structures when stabilized by a large metal atom in the resulting void space. Various atoms that can function as network formers (i.e. form the BO6 octahedra) and void fillers. There are clearly a very large number of possible combinations of the two types and there are several hundreds of compounds known with this structure and many more could no doubt be synthesized.
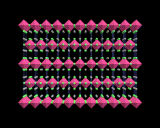
The perovskite structure itself, however, provides crystal chemistry with a platform for more structural diversity and complexity. First, we can distort the structure - a trick that is commonly played with simple, high symmetry structures - and the perovskite structure is especially susceptible to distortions. One of the simplest, commonest and most significant is exemplified by barium titanate. Small distortions of the TiO6 octahedra occur at lower temperatures. These may be described crudely interms of displacements of Ti ions towards corners, edges or faces of the octahedron. The displacements are 'cooperative', that is all the Ti ions move in the same direction. And there are three distorted low temperature structures corresponding to the three directions of the displacements shown.
Because all the ions have moved in the same direction, there is net displacement of electric charge in the crystal, manifested by the crystal having a permanent electrical dipole moment. Such materials are known as ferroelectrics. They have a wide range of uses in the electronic industry. Many other perovskite structured materials show ferroelectric phases at low temperatures; and the range of compounds is so wide that it is often possible, by varying one or both metal atoms, to 'tune' the electrical properties of the material. Indeed solid state scientists have taken this procedure to a fine art; complex mixed metal systems may be synthesized with several different types of metal atom occupying both the octahedral and void sites.
 |
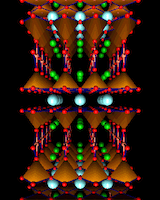
The next ploy in developing more complex structures is to insertlayers of another structural type. In particular, if we insert single layers of the sodium chloride (rock salt) structure into that of perovskites as shown, we generate the now famous crystal structures are adopted by lanthanum copper oxide we create the material which, when 'doped' with Ca or Sr shows the phenomenon of "superconductivity" at much higher temperatures(i.e. ~40K above absolute zero) than had been previously achieved. Indeed discovery of this material by Bednorz and Muller in 1987 stimulated a frenzy of research aimed at synthesizing materials which would show superconductivity at higher and higher temperatures. And within nine months of Bednorz and Muller's sensational discovery, a new material comprising the elements yttrium, barium, copper and oxygen had been synthesized showing superconductivity at ~90K - higher than the temperature at which nitrogen becomes a liquid (offering the possibility of exciting applications as liquid nitrogen cryogenics is relatively cheap). The structure of this remarkable material is shown; it is still a relative - if a more distant one - of the perovskite structure.
 |
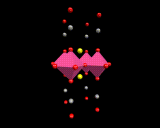
The ultimate goal of this field is 'room temperature' superconductivity;and the race to produce 'warm superconductors' continues unabated. At the time of writing there is a renewed ferment in the field caused by the hint that highly complex structures(containing many layers comprising copper and oxygen atoms might show superconductivity at temperatures approaching thenormal ambient.
 |
And if room temperature superconductivity is achieved, it will be by the solid state chemist - the 'crystal engineer' - modifying and manipulating crystal architectures until the desired physical properties have been achieved.