The Molecular Universe

Tetrahedra and octahedra.

We have already seen simple crystal structures - rocksalt, rutile and many metals - can be understood in terms of packing. The atoms attract each other and pack together in the most efficient manner. The crystal structures are controlled by the relative atomic sizes, which limit the ways in which the atoms can be packed around each other. If all atoms have the same size, then geometrical considerations show that each atom can have twelve surrounding atoms as in the structure of metals; but in rocksalt (sodium chloride) the greater size of the chloride ion means that only six of these can pack round a sodium ion. Indeed, packing considerations like this can be used effectively to guide and rationalise many of the structures adopted by crystals in which the atoms are bound by metallic or electrostatic (ionic) forces.

More complex and less dense structures are commonly adopted by crystals where the bonding has specific directional requirements which is generally the case with covalent bonding - that is bonding based on concentration of the electrons between the nuclei. For these systems, an alternative approach is often needed to understand and describe their structures: instead of packing of spheres, we consider linking of polyhedra; that is, we describe the crystal structure in terms of well defined simple geometrical constructs, e.g. tetrahedra and octahedra with atomic positions normally being associated with their corners and centres; these are then linked together via their corners, edges or faces to give the three dimensional crystal structure.

ReO₃ possesses one of the simplest but most elegant examples of this class of crystal architecture. It displays the structure of the oxide of the rare metal rhenium, which is based on octahedra in which six oxygen atoms surround a central rhenium atom; the octahedra are then linked together via all their corners to give a regular, symmetrical structure.

ReO₃.

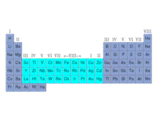
The open nature of the structure is apparent: big voids are present between the octahedrally linked lattice structure into which, as we will describe later, large atoms can be inserted. Indeed, as we will learn, an important type of structure is based on the principle of accommodating atoms in the voids of corner sharing octahedral networks. The formation of MO6 octahedral (where M is a metal atom) dominates the structural chemistry of the oxides of metals such as titanium, vanadium, niobium, tantalum, molybdenum, tungsten and rhenium, which are grouped together in the same region of the periodic table on the left.

The periodic table showing metal atoms which typically possess octahedral coordination with oxygen.

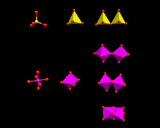
MO₆ octahedral containing these metals may share edges as well as corners, as in the structure of TiO₂ shown on the left. Face sharing is possible, but occurs to only a limited extent owing to the strong repulsions between the positive charges of the closely spaced metal atoms in neighbouring octahedra. Examples are largely limited to small clusters like that on the left. There is indeed a fascinating and diverse structural chemistry based on small aggregates of MO₆ octahedra, some of which are shown in this image.

Polyanion clusters based on octahedrally coordinated metal atoms.

Crystal structures fully exploit the architectural possibilities of octahedral building blocks. The metal niobium forms oxide structures containing blocks of corner shared NbO₆ octahedra, which in turn are linked together by edges or faces as shown.

Nb₂O₅.

Ti5O9.

Moreover, changes in chemical composition can cause restructuring of the octahedral networks. Thus as the oxide material TiO₂ loses oxygen (to form a "non-stoichiometric" compound TiO_2-x) sheets appear in the structure in which face has replaced edge sharing.

The linking of tetrahedra leads to an even bigger range of structures, although the structural principles are in some ways more limited. Tetrahedra normally share only corners, as the repulsion between the central atoms are too high in edge and face shared structures; The image on the left shows examples of the very limited range of structures which contain these latter energetically expensive modes of linkage.

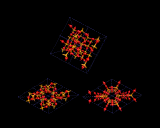
Corner sharing linkage of MO₄ tetrahedra is, however, the basis of the structural chemistry of the oxides of the common and important elements aluminium, silicon and phosphorus. Thus silicon dioxide forms a bewildering range of structures all of which are based on SiO₄ tetrahedral networks in which all corners are shared. The most important is quartz, a natural mineral and an important industrial material. Other structures e.g. cristobalite and tridymite are adopted by SiO₂; and there exists an enormous range of much more open networks e.g. the clathrasils, examples of which are illustrated on the left.

These may accommodate large organic molecules (and indeed their synthesis in most cases requires the presence of such species). Further discussion of these and related 'microporous' structures will follow later. It seems, however, that despite the limitations imposed by the almost universal adoption of corner sharing in tetrahedrally based structures, the tetrahedron allows an even greater diversity of structural types than does the octahedron.

Tetrahedra sharing faces to form a helix.

SiO₂ polymorphs.